Adrien's Neural Network Paper published in Phys. Rev. Applied!
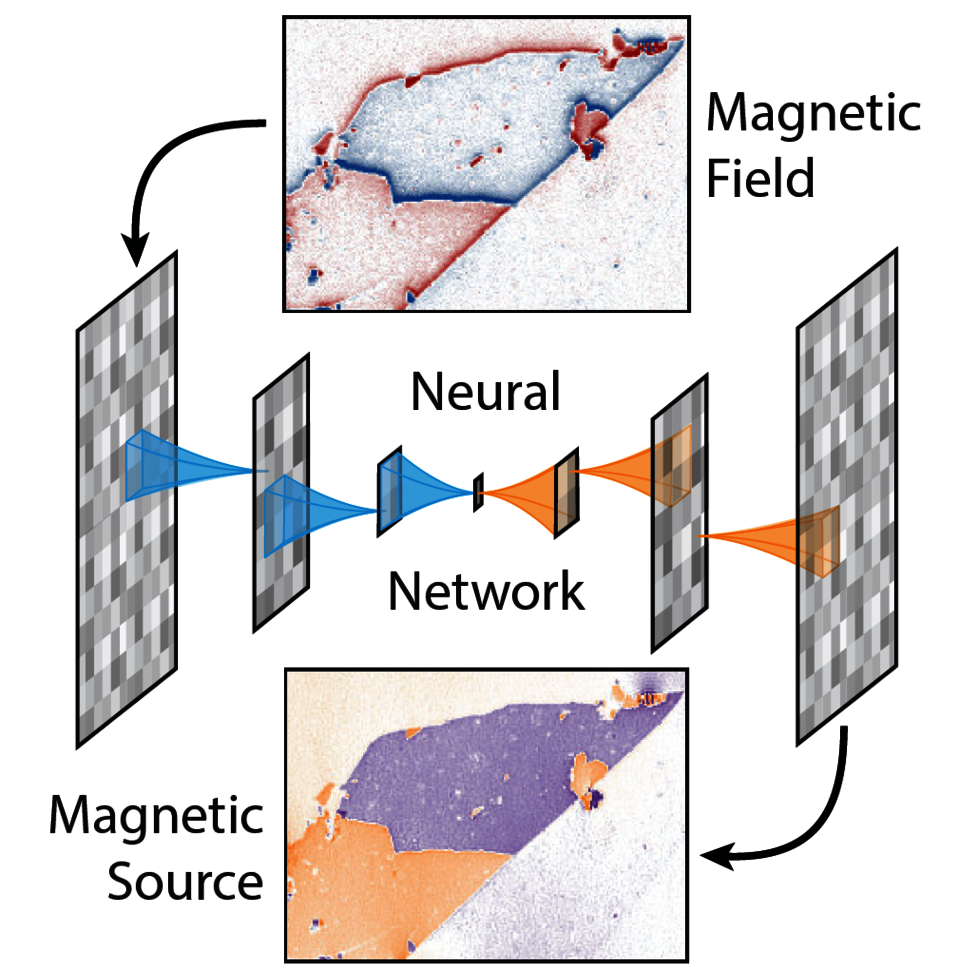
The prediction of measurement outcomes from an underlying structure often follows directly from fundamental physical principles. However, a fundamental challenge is posed when trying to solve the inverse problem of inferring the underlying source configuration based on measurement data. A key difficulty arises from the fact that such reconstructions often involve ill-posed transformations and that they are prone to numerical artifacts. Here, we develop a numerically efficient method to tackle this inverse problem for the reconstruction of magnetization maps from measured magnetic stray-field images. Our method is based on neural networks with physically inferred loss functions to efficiently eliminate common numerical artifacts. We report on a significant improvement in reconstruction over traditional methods and we show that our approach is robust to different magnetization directions, both in and out of plane, and to variations of the magnetic field measurement-axis orientation. While we showcase the performance of our method using magnetometry with nitrogen-vacancy center spins in diamond, our neural-network-based approach to solving inverse problems is agnostic to the measurement technique and thus is applicable beyond the specific use case demonstrated in this work.
Quick Links
