The NV center offers a variety of properties that make it particularly amenable to applications in spin-based quantum sensing and quantum information processing. Most notably, the NV center is a point-like "color center" in diamond, which possesses a non-zero spin in its ground state together with convenient optical methods to initiate, manipulate, and read out this spin.

Each NV center is formed by a nitrogen atom in place of one carbon atom in the diamond crystal lattice, combined with a vacancy in one of the nearest neighboring sites (Fig. 1a). The NV's ground state is a spin-triplet (spin S=1) which consists of three spin-sublevels with spin-projections m_s=0 and ±1 along the N-V axis. The m_s=±1 levels are shifted from ms=0 by a crystal field splitting of Δ=2.87 GHz. Additionally, a magnetic field along the N-V axis will lead to a Zeeman splitting between the m_s=±1 sublevels (this splitting is directly proportional to the external magnetic field).

To understand the principle behind optical spin-readout and initialization, it is instructive to consider a (simplified) scheme of the electronic levels present in an NV center (see Fig.1b). Each NV spin-state in the orbital ground state is linked by optical transitions ("wavy" arrows) to corresponding spin-states in an orbital excited state with typical radiative lifetimes of 20 ns. These optical transitions are highly spin-preserving, i.e. they hardly alter m_s during a direct optical excitation-deexcitation cycle. However, in addition to such direct optical coupling, the excited m_s=±1 states have a non-zero probability (~50 % under typical conditions) to decay non-radiatively into a metastable singlet state in which they remain "trapped" for a few hundreds of nanoseconds before decaying selectively into the m_s=0 orbital ground-state. These different relaxation pathways have two immediate consequences:

1. Under continuous optical excitation, the NV center is automatically spin-pumped into m_s=0.
2. The fluorescence rate of the NV center changes as a function of the NV's spin-state. If initially m_s=±1, the NV will soon decay into the singlet state and remain "dark". In contrast, if m_s=0, the NV will continuously emit photons under optical excitation and be "bright".

This picture has been verified by a variety of experiments. A most direct experimental manifestation of this level-scheme is the possibility to observe optically detected Electron Spin Resonance (ESR). Under continuous optical excitation (typically using green light as indicated in Fig. 1b), the NV center is polarized into m_s=0. If additionally a time-varying magnetic field with frequency ω_MW (typically in the microwave range) is applied and if ω_MW is resonant with either the m_s=0 → -1 or 0 → +1 transition, this microwave-field will populate m_s=-1 or +1 and correspondingly lead to a reduction in detected NV fluorescence-counts. Such an experiment is shown in Fig. 1c and demonstrates the efficient way in which NV spins can be read-out optically.

Building on these basic NV-properties, one can perform a variety of experiments to manipulate and study the NV spin. Most notably, coherent NV spin control can be employed to study (and extend) the phase-coherence of the NV spin. Fig. 1d shows an exemple of an NV coherence decay curve as obtained through a Hahn-echo pulse sequence. This exemple yields a spin-coherence time T₂~75μs, but T₂-times of up to 2 ms [5] have been reported under ambient conditions!

Figure 1: Basic spin and optical properties of Nitrogen-Vacancy (NV) centers. (a) Atomic structure and (b) electronic level structure of the NV center. "Wavy" arrows indicate optical transitions between electronic ground and excited states. Blue straight lines indicate non-radiative relaxation. (c) Optically detected Electron Spin Resonance (ESR) in a single NV center. (d) Coherence decay trace of a single NV center measured using a "Spin-echo" sequence. The resulting NV coherence time (T₂) was ~75 μs (here, measured at room temperature for a "scanning NV center").

As early as 1996, it was realized [1] that individual quantum systems could offer a powerful approach for imaging with nanometric spatial resolution. The basic idea was to use an isolated quantum system as a sensor for scanning probe imaging. If this probe is brought in close proximity (distance, d) to a sample, imaging resolution would be given merely by d since the lateral extent of most quantum systems could safely be assumed to be negligible. This original approach was formulated for optical imaging applications and in particular on "Förster resonant energy transfer"-imaging using a scanning, atom-like emitter coupled to an optically active sample. However, it soon became clear that the same principle could be harnessed to obtain nanometric spatial resolution in magnetic imaging [2]. There, instead of optical coupling, magnetic coupling of a scanning single quantum system to a sample of interest is being exploited. In this case again, spatial resolution is given by d, while magnetic sensitivity is determined by the properties of the sensory quantum system, notably it's spin coherence times and the spin-readout efficiency.

While many quantum systems are in principle suitable for this task, the NV center in diamond offers properties that make it particularly useful as a magnetic sensor [3]. Specifically, efficient optical NV spin readout combined with long NV spin coherence times, even at room temperature, render the NV center an attractive candidate for magnetic imaging and sensing applications. A generic method for magnetic field measurements consists of a Ramsey pulse sequence (Fig. 2a): An NV electronic spin is prepared via optical pumping and a π/2-ESR pulse in a superposition of the ms = 0 and ms = 1 states and then left to evolve freely for a time τ. In the presence of a magnetic field, B, the electronic spin evolves (rotates), acquiring a phase ΔΦ=Δτgμ_BB (with μ_B the Bohr magneton and g=2). This phase, and thus the magnetic field, can be measured by projecting the NV electronic spin back onto its quantization-axis and determining the relative ms=0 and ms=1 populations. It can be shown [3] that the resulting magnetic field sensitivity, η_B, is optimized for τ~T₂*, where T₂* is the inhomogeneous spin dephasing time; in this situation, η_B is directly proportional to 1/T₂*. Typical values for NV centers yield T₂*~1 μs and B~1 μT Hz^½. Using more complex spin-manipulation-schemes ("Hahn-echo" [6], "CPMG",...), inhomogeneous spin-dephasing can be avoided, effectively prolonging NV spin-coherence to the homogeneous spin dephasing-time, T₂. Since T₂ can exceed T₂* by several orders of magnitude and since η_B scales as (T₂*/T₂)^½ [3], η_B can be dramatically increased with this method, typically yielding η_B~30 nT Hz^½ for T₂~1 ms. Importantly, the NV center is now sensitive only to time-varying ("AC") magnetic fields that oscillate at the frequency of the applied pulse-sequence (Fig. 2b).

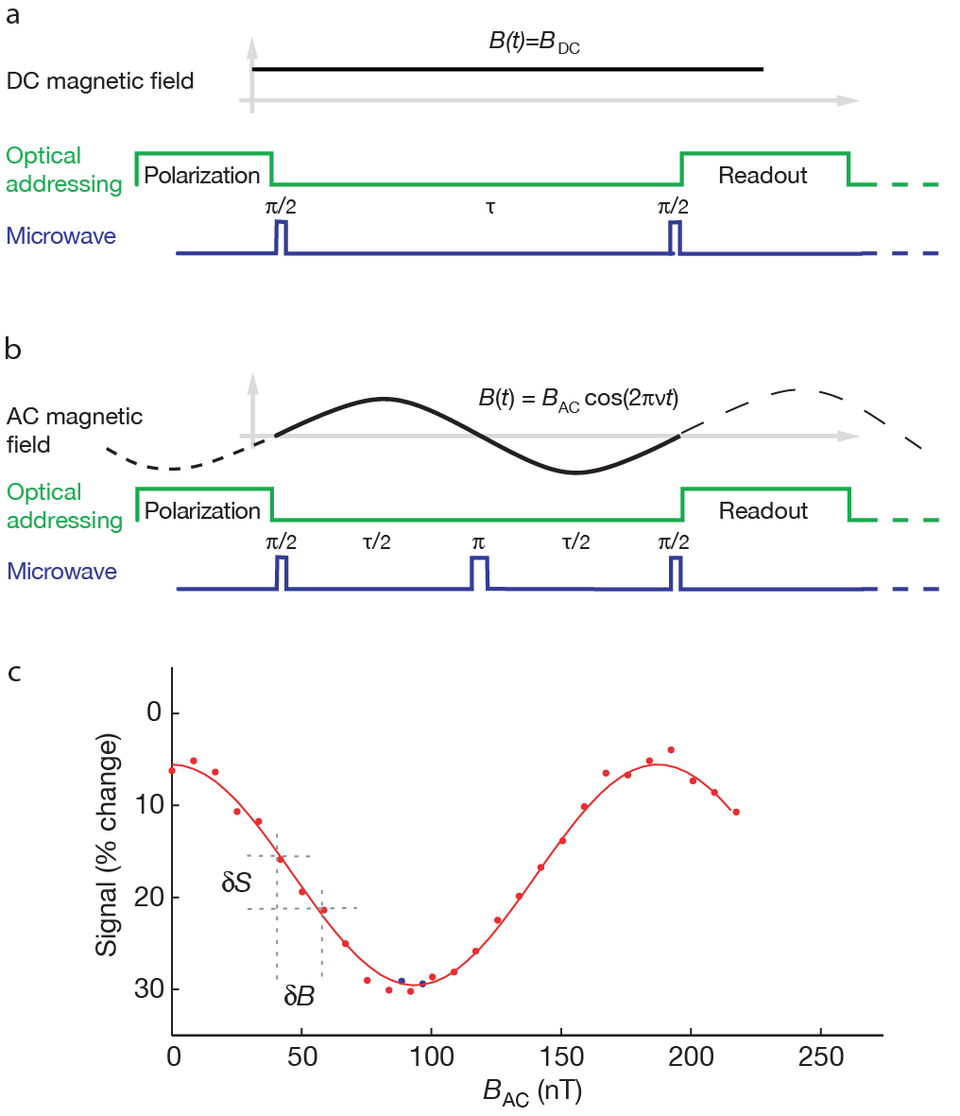
Figure 2: NV magnetometry sequences. (a) "DC-magnetometry" using a Ramsey pulse sequence on the NV spin. Optical excitation is used to initialize and measure the NV spin. During free evolution, the spin acquires a phase ΔΦ=Δτgμ_BB, with τ the total evolution time, μ_B the Bohr magneton and g=2. (b) "AC magnetometry" using a Hahn-echo sequence. The phase is accumulated similar to (a), but the spin-echo sequence allows for a longer T₂ before decoherence affects the readout contrast, C. (c) Experimental results for AC magnetometry. δB/δS determines the NV's sensitivity to changes in B_AC and is directly proportional to η_B. This Figure is adapted from [6].